
Comic Transcript
Panel 1.
Granddaughter: It looks like planets travel in circular orbits.
Alkina: Well, not exactly, they actually travel in ellipses.
Panel 2.
Alkina: A circle is a very specific kind of ellipse, and the orbits of these planets are very close to being circular.
Panel 3.
Alkina: Sometimes objects like asteroids and even some planets can have orbits that aren’t very circular at all.
Panel 4.
Alkina: Of course, there is more to planetary orbits than just that…
Granddaughter: Like what?
Panel 5.
Epo: Objects also travel faster as they get closer to the stars they orbit
Panel 6.
Epo: And their distance from the star is related to how long it takes them to complete an orbit.
What does it mean?
Ellipse – is a closed shape with two focal points such that the sum of the distances from the edge to the points is constant.
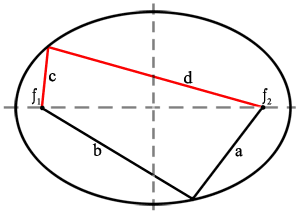
f1 and f2 are the two focal points, or foci of this ellipse. The sum of line segments a and b is equal to the sum of line segments c and d.
Orbit – is the path followed by a moon, planet or artificial satellite as it travels around another body in space.
In human speak please!
A circle is a special type of ellipse. If you take the image above and move the focal points of the ellipse together, the image will become a circle when the focal points (foci) are right on top of each other.
There are certain rules that govern the orbits of planets and other objects in the solar system. These rules were first expressed by Johannes Kepler, a German mathematician and astronomer. These rules are known as Kepler’s Laws of Planetary Motion and state:
- The orbit of every planet is an ellipse with the Sun at one of the foci.
- An imaginary line joining a planet and the Sun sweeps out equal areas during equal intervals of time.
- The time it takes a planet to orbit the Sun is related to how far away from the Sun an object is. (This means that the larger the average distance from the Sun, the longer it takes for an object to orbit it.)
The period (time) that Earth takes to go around the Sun is about 365 days or 1 year. For Jupiter, which is farther away (about 5 times the average distance of Earth to the Sun), the period is 11.86 years. Check out the video in the multimedia section below to see these laws in action.
Is that all?
Johannes Kepler: His Life, His Laws and Times – Kepler’s biography.
